kruskal wallis test research paper

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Nonparametric statistical tests for the continuous data: the basic concept and the practical use

Francis sahngun nahm.

• Author information
• Article notes
• Copyright and License information

Corresponding author: Francis Sahngun Nahm, M.D. Department of Anesthesiology and Pain Medicine, Seoul National University Bundang Hospital, 82, Gumi-ro 173 Beon-gil, Bundang-gu, Seongnam 13620, Korea. Tel: 82-31-787-7499, Fax: 82-31-787-4063, [email protected]

Corresponding author.

Received 2015 Dec 7; Revised 2015 Dec 28; Accepted 2015 Dec 28; Issue date 2016 Feb.

This is an open-access article distributed under the terms of the Creative Commons Attribution Non-Commercial License ( http://creativecommons.org/licenses/by-nc/4.0/ ), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Conventional statistical tests are usually called parametric tests. Parametric tests are used more frequently than nonparametric tests in many medical articles, because most of the medical researchers are familiar with and the statistical software packages strongly support parametric tests. Parametric tests require important assumption; assumption of normality which means that distribution of sample means is normally distributed. However, parametric test can be misleading when this assumption is not satisfied. In this circumstance, nonparametric tests are the alternative methods available, because they do not required the normality assumption. Nonparametric tests are the statistical methods based on signs and ranks. In this article, we will discuss about the basic concepts and practical use of nonparametric tests for the guide to the proper use.

Keywords: Data interpretation, Investigative technique, Nonparametric statistics, Statistical data analysis

Introduction

Statistical analysis is a universal method with which to assess the validity of a conclusion. It is one of the most important aspects of a medical paper. Statistical analysis grants meaning to otherwise meaningless series of numbers and allow researchers to draw conclusions from uncertain facts. Hence, it is a work of creation that breathes life into data. However, the inappropriate use of statistical techniques results in faulty conclusions, inducing errors and undermining the significance of the article. Moreover, medical researchers must pay more attention to acquiring statistical validity as evidence-based medicine has taken center stage on the medicine scene in these days. Recently, rapid advances in statistical analysis packages have opened doors to more convenient analyses. However, easier methods of performing statistical analyses, such as inputting data on software and simply pressing the "analysis" or "OK" button to compute the P value without understanding the basic concepts of statistics, have increased the risk of using incorrect statistical analysis methods or misinterpreting analytical results [ 1 ].

Several journals, including the Korean Journal of Anesthesiology , have been striving to identify and to reduce statistical errors overall in medical journals [ 2 , 3 , 4 , 5 ]. As a result, a wide array of statistical errors has been found in many papers. This has further motivated the editors of each journal to enhance the quality of their journals by developing checklists or guidelines for authors and reviewers [ 6 , 7 , 8 , 9 ] to reduce statistical errors. One of the most common statistical errors found in journals is the application of parametric statistical techniques to nonparametric data [ 4 , 5 ]. This is presumed to be due to the fact that medical researchers have had relatively few opportunities to use nonparametric statistical techniques as compared to parametric techniques because they have been trained mostly on parametric statistics, and many statistics software packages strongly support parametric statistical techniques. Therefore, the present paper seeks to boost our understanding of nonparametric statistical analysis by providing actual cases of the use of nonparametric statistical techniques, which have only been introduced rarely in the past.

The History of Nonparametric Statistical Analysis

John Arbuthnott, a Scottish mathematician and physician, was the first to introduce nonparametric analytical methods in 1710 [ 10 ]. He performed a statistical analysis similar to the sign test used today in his paper "An Argument for divine providence, taken from the constant regularity observ'd in the Births of both sexes." Nonparametric analysis was not used for a while after that paper, until Jacob Wolfowitz used the term "nonparametric" again in 1942 [ 11 ]. Then, in 1945, Frank Wilcoxon introduced a nonparametric analysis method using rank, which is the most commonly used method today [ 12 ]. In 1947, Henry Mann and his student Donald Ransom Whitney expanded on Wilcoxon's technique to develop a technique for comparing two groups of different number of samples [ 13 ]. In 1951, William Kruskal and Allen Wallis introduced a nonparametric test method to compare three or more groups using rank data [ 14 ]. Since then, several studies have reported that nonparametric analyses are just as efficient as parametric methods; it is known that the asymptotic relative efficiency of nonparametric statistical analysis, specifically Wilcoxon's signed rank test and the Mann-Whitney test, is 0.955 against the t-test when the data satisfies the assumption of normality [ 15 , 16 ]. Ever since when Tukey developed a method to compute confidence intervals using a nonparametric method, nonparametric analysis was established as a commonly used analytical method in medical and natural science research [ 17 ].

The Basic Principle of Nonparametric Statistical Analysis

Traditional statistical methods, such as the t-test and analysis of variance, of the types that are widely used in medical research, require certain assumptions about the distribution of the population or sample. In particular, the assumption of normality, which specifies that the means of the sample group are normally distributed, and the assumption of equal variance, which specifies that the variances of the samples and of their corresponding population are equal, are two most basic prerequisites for parametric statistical analysis. Hence, parametric statistical analyses are conducted on the premise that the above assumptions are satisfied. However, if these assumptions are not satisfied, that is, if the distribution of the sample is skewed toward one side or the distribution is unknown due to the small sample size, parametric statistical techniques cannot be used. In such cases, nonparametric statistical techniques are excellent alternatives.

Nonparametric statistical analysis greatly differs from parametric statistical analysis in that it only uses + or - signs or the rank of data sizes instead of the original values of the data. In other words, nonparametric analysis focuses on the order of the data size rather than on the value of the data per se. For example, let's pretend that we have the following five data for a variable X.

After listing the data in the order of their sizes, each instance of data is ranked from one to five; the data with the lowest value (18) is ranked 1, and the data with the greatest value (99) is ranked 5. There are two data instances with values of 32, and these are accordingly given a rank of 2.5. Furthermore, the signs assigned to each data instance are a + for those values greater than the reference value and a − for those values less than the reference value. If we assign a reference value of 50 for these instances, there would only be one value greater than 50, resulting in one + and four − signs. While parametric analysis focuses on the difference in the means of the groups to be compared, nonparametric analysis focuses on the rank, thereby putting more emphasis differences of the median values than the mean.

As shown above, nonparametric analysis converts the original data in the order of size and only uses the rank or signs. Although this can result in a loss of information of the original data, nonparametric analysis has more statistical power than parametric analysis when the data are not normally distributed. In fact, as shown in the above example, one particular feature of nonparametric analysis is that it is minimally affected by extreme values because the size of the maximum value (99) does not affect the rank or the sign even if it is greater than 99.

Advantages and Disadvantages of Nonparametric Statistical Analysis

Nonparametric statistical techniques have the following advantages:

- There is less of a possibility to reach incorrect conclusions because assumptions about the population are unnecessary. In other words, this is a conservative method.

- It is more intuitive and does not require much statistical knowledge.

- Statistics are computed based on signs or ranks and thus are not greatly affected by outliers.

- This method can be used even for small samples.

On the other hand, nonparametric statistical techniques are associated with the following disadvantages:

- Actual differences in a population cannot be known because the distribution function cannot be stated.

- The information acquired from nonparametric methods is limited compared to that from parametric methods, and it is more difficult to interpret it.

- Compared to parametric methods, there are only a few analytical methods.

- The information in the data is not fully utilized.

- Computation becomes complicated for a large sample.

In summary, using nonparametric analysis methods reduces the risk of drawing incorrect conclusions because these methods do not make any assumptions about the population, whereas can have lower statistical power. In other words, nonparametric methods are "always valid, but not always efficient," while parametric methods are "always efficient, but not always valid." Therefore, parametric methods are recommended when they can in fact be used.

Types of Nonparametric Statistical Analyses

In this section, I explain the median test for one sample, a comparison of two paired samples, a comparison of two independent samples, and a comparison of three or more samples. The types of nonparametric analysis techniques and the corresponding parametric analysis techniques are delineated in Table 1 .

Table 1. Analog of Parametic and Nonparametric Tests.

Median test for one sample: the sign test and wilcoxon's signed rank test.

The sign test and Wilcoxon's signed rank test are used for median tests of one sample. These tests examine whether one instance of sample data is greater or smaller than the median (reference value).

The sign test is the simplest test among all nonparametric tests regarding the location of a sample. This test examines the hypothesis about the median θ 0 of a population, and it involves testing the null hypothesis H 0 : θ = θ 0 . If the observed value (X i ) is greater than the reference value (θ 0 ), it is marked as +, and it is given a − sign if the observed value is smaller than the reference value, after which the number of + values is calculated. If there is an observed value in the sample that is equal to the reference value (θ 0 ), the said observed value is eliminated from the sample. Accordingly, the size of the sample is then reduced to proceed with the sign test. The number of sample data instances given the + sign is denoted as 'B' and is referred to as the sign statistic. If the null hypothesis is true, the number of + signs and the number of − signs are equal. The sign test ignores the actual values of the data and only uses + or − signs. Therefore, it is useful when it is difficult to measure the values.

Wilcoxon's signed rank test

The sign test has one drawback in that it may lead to a loss of information because only + or − signs are used in the comparison of the given data with the reference value of θ 0 . In contrast, Wilcoxon's signed rank test not only examines the observed values in comparison with θ 0 but also considers the relative sizes, thus mitigating the limitation of the sign test. Wilcoxon's signed rank test has more statistical power because it can reduce the loss of information that arises from only using signs. As in the sign test, if there is an observed value that is equal to the reference value θ 0 , this observed value is eliminated from the sample and the sample size is adjusted accordingly. Here, given a sample with five data points (X i ), as shown in Table 2 , we test whether the median (θ 0 ) of this sample is 50.

Table 2. Examples of Sign Test and Wilcoxon's Singed Rank Test for One Sample.

Let the median (θ 0 ) is 50. The original data were transformed into rank and sign data. +/- mean X i > 50 and < 50 respectively. The round bracket means rank.

In this case, if we subtract θ 0 from each data point (R i = X i - θ 0 ), find the absolute value, and rank the values in increasing order, the resulting rank is equal to the value in the parenthesis in Table 2 . With Wilcoxon's signed rank test, only the ranks with positive values are added as per the following equation:

Comparison of a paired sample: sign test and Wilcoxon's signed rank test

In the previously described one-sample sign test, the given data was compared to the median value (θ 0 ). The sign test for a paired sample compares the scores before and after treatment, with everything else identical to how the one-sample sign test is run. The sign test does not use ranks of the scores but only considers the number of + or − signs. Thus, it is rarely affected by extreme outliers. At the same time, it cannot utilize all of the information in the given data. Instead, it can only provide information about the direction of the difference between two samples, but not about the size of the difference between two samples.

This test is a nonparametric method of a paired t test. The only difference between this test and the previously described one-sample test is that the one-sample test compares the given data to the reference value (θ 0 ), while the paired test compares the pre- and post-treatment scores. In the example with five paired data instances (X ij ), as shown in Table 3 , which shows scores before and after education, X 1j refers to the pre-score of student j, and X 2j refers to the post-score of student j. First, we calculate the change in the score before and after education (R j = X 1j - X 2j ). When R j is listed in the order of its absolute values, the resulting rank is represented by the values within the parentheses in Table 3 . Wilcoxon's signed rank test is then conducted by adding the number of + signs, as in the one-sample test. If the null hypothesis is true, the number of + signs and the number of − signs should be nearly equal.

Table 3. Example of Wilcoxon's Singed Rank Test for the Paired Sample.

Under the null hypothesis (no difference between the pre/post scores), test statistics (W + , the sum of the positive rank) would be close to 7.5 ( = ∑ k = 1 5 k 2 ), but get far from 7.5 when the alternative hypothesis is true. According to the table for Wilcoxon's rank sum test, the P value = 0. 1363 when test statistics (W + ) 3 under α = 0.05 (two tailed test) and the sample size = 5. Therefore, null hypothesis cannot be rejected.

The sign test is limited in that it cannot reflect the degree of change between paired scores. Wilcoxon's signed rank test has more statistical power than the sign test because it not only considers the direction of the change but also ranks the degree of change between the paired scores, providing more information for the analysis.

Comparison of two independent samples: Wilcoxon's rank sum test, the Mann-Whitney test, and the Kolmogorov-Smirnov test

Wilcoxon's rank sum test and mann-whitney test.

Wilcoxon's rank sum test ranks all data points in order, calculates the rank sum of each sample, and compares the difference in the rank sums ( Table 4 ). If two groups have similar scores, their rank sums will be similar; however, if the score of one group is higher or lower than that of the other group, the rank sums between the two groups will be farther apart.

Table 4. Examples and Process of Wilcoxon's Rank Sum Test.

There are two independent groups with the sample sizes of group X (m) is 5 and group Y (n) is 4. Under the null hypothesis (no difference between the 2 groups), the rank sum of group X (W X ) and group Y (W Y ) would be close to 22.5 ( = ∑ k = 1 9 k 2 , but get far from 22.5 when the alternative hypothesis is true. According to the table for Wilcoxon's rank sum test, the P value = 0. 0556 when test statistics (W Y ) = 13 under α = 0.05 (two tailed test) at m = 5 and n = 4. Therefore, null hypothesis cannot be rejected.

On the other hand, the Mann-Whitney test compares all data x i belonging in the X group and all data y i belonging in the Y group and calculates the probability of xi being greater than y i : P(x i > y i ). The null hypothesis states that P(x i > y i ) = P(x i < y i ) = ½, while the alternative hypothesis states that P(x i > y i ) ≠ ½. The process of the Mann-Whitney test is illustrated in Table 5 . Although the Mann-Whitney test and Wilcoxon's rank sum test differ somewhat in their calculation processes, they are widely considered equal methods because they use the same statistics.

Table 5. Example and Process of Mann-Whitney Test.

There are two independent groups with the sample sizes of group X (m) is 5 and group Y (n) is 4. Under the null hypothesis (no difference between the 2 groups), the test statistics (U) gets closer to 10 ( = m × n 2 ), but gets more extreme (smaller in this example) when the alternative hypothesis is true. The test statistics of this data is U = 3, which is greater than the reference value of 1 under α = 0.05 (two tailed test) at m = 5 and n = 4. Therefore, null hypothesis cannot be rejected.

Kolmogorov-Smirnov test (K-S test)

The K-S test is commonly used to examine the normality of a data set. However, it is originally a method that examines the cumulative distributions of two independent samples to examine whether the two samples are extracted from two populations with an equal distribution or the same population. If they were extracted from the same population, the shapes of their cumulative distributions would be equal. In contrast, if the two samples show different cumulative distributions, it can be assumed that they were extracted from different populations. Let's use the example in Table 6 for an actual analysis. First, we need to identify the distribution pattern of two samples in order to compare two independent samples. In Table 6 , the range of the samples is 43 with a minimum value of 50 and a maximum value of 93. The statistical power of the K-S test is affected by the interval that is set. If the interval is too wide, the statistical power can be reduced due to a small number of intervals; similarly, if the interval is too narrow, the calculations become too complicated due to the excessive number of intervals. The data shown in Table 6 has a range of 43; hence, we will establish an interval range of 4 and set the number of intervals to 11. As shown in Table 6 , a cumulative probability distribution table must be created for each interval (S X , S Y ), and the value with the greatest difference between the cumulative distributions of two variables (Max(S X - S Y )) must be determined. This maximum difference is the test statistic. We compare this difference to the reference value to test the homogeneity of the two samples. The actual analysis process is described in Table 6 .

Table 6. Example and Process of Kolmogorov-Smirnov Test.

There are two independent groups with the sample sizes of group X (N X ) and group Y (N Y ) are 15. The maximal difference between the cumulative probability density of X (S X ) and Y (S Y ) is 8/15 (0.533), which is greater than the rejection value of 0.467 under α = 0.05 (two tailed test) at N X = N Y = 15. Therefore, there is a significant difference between the group X and group Y.

Comparison of k independent samples: the Kruskal-Wallis test and the Jonckheere test

Kruskal-wallis test.

The Kruskal-Wallis test is a nonparametric technique with which to analyze the variance. In other words, it analyzes whether there is a difference in the median values of three or more independent samples. The Kruskal-Wallis test is similar to the Mann-Whitney test in that it ranks the original data values. That is, it collects all data instances from the samples and ranks them in increasing order. If two scores are equal, it uses the average of the two ranks to be given. The rank sums are then calculated and the Kruskal-Wallis test statistic (H) is calculated as per the following equation [ 14 ]:

Jonckheere test

Greater statistical power can be acquired if a rank alternative hypothesis is established using prior information. Let's think about a case in which we can predict the order of the effects of a treatment when increasing the degree of the treatment. For example, when we are evaluating the efficacy of an analgesic, we can predict that the effect will increase depending on the dosage, dividing the groups into a control group, a low-dosage group, and a high-dosage group. In this case, the null hypothesis H 2 is better than the null hypothesis H 1 .

H 0 : [τ 1 = τ 2 = τ 3 ]

H 1 : [τ 1 , τ 2 , τ 3 not all equal]

H 2 : [τ 1 ≤ τ 2 ≤ τ 3 , with at least strict inequality]

The Jonckheere test is a nonparametric technique that can be used to test such a rank alternative hypothesis [ 18 ].

The actual analysis process is described with illustration in Table 7 .

Table 7. Example and Process of Jonckheere Test.

The test statistic J = 55 and P (J ≥ 55) = 0.035. Therefore, the null hypothesis (τ 1 = τ 2 = τ 3 ) is rejected and the alternative hypothesis (τ 1 ≤ τ 2 ≤ τ 3 , with at least strict inequality) is accepted under α = 0.05.

Nonparametric tests and parametric tests: which should we use?

As there is more than one treatment modality for a disease, there is also more than one method of statistical analysis. Nonparametric analysis methods are clearly the correct choice when the assumption of normality is clearly violated; however, they are not always the top choice for cases with small sample sizes because they have less statistical power compared to parametric techniques and difficulties in calculating the "95% confidence interval," which assists the understanding of the readers. Parametric methods may lead to significant results in some cases, while nonparametric methods may result in more significant results in other cases. Whatever methods can be selected to support the researcher's arguments most powerfully and to help the reader's easy understandings, when parametric methods are selected, researchers should ensure that the required assumptions are all satisfied. If this is not the case, it is more valid to use nonparametric methods because they are "always valid, but not always efficient," while parametric methods are "always efficient, but not always valid".

• 1. Rosenbaum SH. Statistical methods in anesthesia. In: Miller RD, editor. Miller's Anesthesia. 7th ed. Philadelphia: Elsevier Inc; 2010. pp. 3075–3086. [ Google Scholar ]
• 2. Ko H, Kwak IY, Kim KW, Ham BM, Choe IH. Statistical methods in the articles of the journal of the Korean society of anesthesiologists from 1981 to 1990. Korean J Anesthesiol. 1993;26:22–27. [ Google Scholar ]
• 3. Hwang K, Lee HJ, Kim YJ, Lee SI. Statistical errors in papers in the journal of Korean society of plastic and reconstructive surgeons. J Korean Soc Plast Reconstr Surg. 2001;28:302–309. [ Google Scholar ]
• 4. Yim KH, Nahm FS, Han KA, Park SY. Analysis of statistical methods and errors in the articles published in the Korean journal of pain. Korean J Pain. 2010;23:35–41. doi: 10.3344/kjp.2010.23.1.35. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 5. Ahn W. Statistical methods in the articles in the Korean journal of anesthesiology published from 1994 to 1998. Korean J Anesthesiol. 2000;39:706–711. [ Google Scholar ]
• 6. Altman DG, Gore SM, Gardner MJ, Pocock SJ. Statistical guidelines for contributors to medical journals. Br Med J (Clin Res Ed) 1983;286:1489–1493. doi: 10.1136/bmj.286.6376.1489. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 7. Gardner MJ, Machin D, Campbell MJ. Use of check lists in assessing the statistical content of medical studies. Br Med J (Clin Res Ed) 1986;292:810–812. doi: 10.1136/bmj.292.6523.810. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 8. Ahn YO, Lee HK. Development of a checklist for assessing the metholological and statistical validity of medical articles. Korean J Med Educ. 1991;3:19–35. [ Google Scholar ]
• 9. Lee S, Kang H. Statistical and methodological considerations for reporting RCTs in medical literature. Korean J Anesthesiol. 2015;68:106–115. doi: 10.4097/kjae.2015.68.2.106. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 10. Arbuthnott J. An argument for divine providence, taken from the constant regularity Observ'd in the births of both sexes. Philos Trans R Soc Lond. 1710;27:186–190. [ Google Scholar ]
• 11. Wolfowitz J. Additive partition functions and a class of statistical hypotheses. Ann Math Stat. 1942;13:247–279. [ Google Scholar ]
• 12. Wilcoxon F. Individual comparisons by ranking methods. Biom Bull. 1945;1:80–83. [ Google Scholar ]
• 13. Mann HB, Whitney DR. On a test of whether one of two random variables is stochastically larger than the other. Ann Math Stat. 1947;18:50–60. [ Google Scholar ]
• 14. Kruskal WH, Wallis WA. Use of ranks in one-criterion variance analysis. J Am Stat Assoc. 1952;47:583–621. [ Google Scholar ]
• 15. Hodges JL, Jr, Lehmann EL. The efficiency of some nonparametric competitors of the t-test. Ann Math Stat. 1956;27:324–335. [ Google Scholar ]
• 16. Chernoff H, Savage IR. Asymptotic normality and efficiency of certain nonparametric test statistics. Ann Math Stat. 1958;29:972–994. [ Google Scholar ]
• 17. Tukey JW. Bias and confidence in not-quite large samples. Ann Math Stat. 1958;29:614. [ Google Scholar ]
• 18. Jonckheere AR. A distribution-free k-sample test against ordered alternatives. Biometrika. 1954;41:133–145. [ Google Scholar ]
• View on publisher site
• PDF (631.2 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

• Open access
• Published: 17 October 2021

Analysis of COVID-19 data using neutrosophic Kruskal Wallis H test

• Rehan Ahmad Khan Sherwani 1 ,
• Huma Shakeel 1 ,
• Wajiha Batool Awan 1 ,
• Maham Faheem 1 &
• Muhammad Aslam   ORCID: orcid.org/0000-0003-0644-1950 2  

BMC Medical Research Methodology volume  21 , Article number:  215 ( 2021 ) Cite this article

16k Accesses

30 Citations

Metrics details

Kruskal-Wallis H test from the bank of classical statistics tests is a well-known nonparametric alternative to a one-way analysis of variance. The test is extensively used in decision-making problems where one has to compare the equality of several means when the observations are in exact form. The test is helpless when the data is in an interval form and has some indeterminacy.

The interval-valued data often contain uncertainty and imprecision and often arise from situations that contain vagueness and ambiguity. In this research, a modified form of the Kruskal-Wallis H test has been proposed for indeterminacy data. A comprehensive theoretical methodology with an application and implementation of the test has been proposed in the research.

The proposed test is applied on a Covid-19 data set for application purposes. The study results suggested that the proposed modified Kruskal-Wallis H test is more suitable in interval-valued data situations. The application of this new neutrosophic Kruskal-Wallis test on the Covid-19 data set showed that the proposed test provides more relevant and adequate results. The data representing the daily ICU occupancy by the Covid-19 patients were recorded for both determinate and indeterminate parts. The existing nonparametric Kruskal-Wallis H test under Classical Statistics would have given misleading results. The proposed test showed that at a 1% level of significance, there is a statistically significant difference among the average daily ICU occupancy by corona-positive patients of different age groups.

Conclusions

The findings of the results suggested that our proposed modified form of the Kruskal-Wallis is appropriate in place of the classical form of the test in the presence of the neutrosophic environment.

Peer Review reports

Introduction

Hypothesis testing is a scientific process used to investigate the acceptance or rejection of a proposition under consideration. Two approaches are used in statistics to verify a hypothesis: 1) Parametric approach 2) Nonparametric approach. The most important aspect of the parametric approach is the satisfaction of the assumption about data’s normality, and a few tests require the equality of population variances [ 1 ]. In most situations, the distributional assumption under a parametric test hardly satisfy, and the use of nonparametric or distribution-free tests is a common practice [ 2 , 3 ]. However, all such nonparametric tests apply to data containing determined observations. In real life, there are various scenarios where we have non-precise data, and in such cases, the existing hypothesis testing approach based on classical test statistics cannot be implemented. Recent studies have suggested nonparametric tests based on interval-valued data and fuzzy logic [ 4 ]. Smarandache [ 5 ] generalized the fuzzy logic in the neutrosophic sense by considering the interval-valued data and the measure of indeterminacy or falseness. Smarandache introduced Neutrosophic Statistics as a generalization of classical statistics applied when the data under consideration is in neutrosophic numbers [ 6 ]. Smarandache and Khalid [ 6 ] verified the efficiency of neutrosophic logic. Several authors have implemented neutrosophic logic for data containing uncertainty and vagueness; see ref [ 7 , 8 , 9 , 10 , 11 ].

Furthermore, several authors have developed statistical tests to analyze fuzzy data; see, for example, refs [ 12 , 13 , 14 , 15 ]. Also, in fuzzy logic and neutrosophic statistics, several research works have been contributed by introducing decision-making analysis for the data set containing uncertainty and vagueness [ 16 , 17 , 18 ]. Recently, Aslam introduced different statistical tests using Neutrosophic Statistics, including the tests of homogeneity of variance for uncertainty environment, the goodness of fit test in the presence of uncertain parameters, and the Kolmogorov-Smirnov tests under uncertainty [ 19 , 20 , 21 ].

In 1952, Kruskal and Wallis [ 12 ] provided a robust rank-based test for the k sample problem as an alternative to the parametric approaches, such as the one-way analysis of variance (ANOVA). Kruskal-Wallis H test has been used for analysis purposes in various manners; for example, see refs [ 13 , 14 , 15 , 16 , 17 , 18 ]. In the classical k sample problem, data are determined and do not contain any ambiguity or vagueness. However, in many current scientific studies, the observations are not necessarily relentless, and indeterminate parts quantitatively express the uncertainties in a sample. The existing Kruskal-Wallis H test cannot be used to investigate the data which is measured in the neutrosophic intervals. A detailed literature review has given a shred of clear evidence that no such test is available that can be useful as a nonparametric alternate for ANOVA under an indeterminate environment. The unavailability of a method for the said purpose is a source of motivation for the current research. The goal is to develop a test that compares several sample observations or group(s); the proposed test is easy to apply and understandable. The proposed modified Kruskal-Wallis test results in the interval-valued form and is preferable for data containing vagueness and uncertainty. The objectives of this article are (1) to introduce the modified neutrosophic Kruskal Wallis test; (2) to define the methodology of the neutrosophic Kruskal Wallis test; and (3) to compare the performance of the existing Kruskal Wallis test with the proposed test through an application on Covid-19 data set under Neutrosophy. More information about the application of neutrosophic statistics can be seen in [ 22 , 23 , 24 ].

The article is planned as follows. Section 2 presents the computational method for the application of the neutrosophic Kruskal Wallis test. In section 3, the modified Kruskal Wallis test has been demonstrated with an eloquent example of the Covid-19 data set for scrutinizing its efficiency and competence. It is anticipated that the modified nonparametric Kruskal Wallis test will proficiently analyze the data in the presence of uncertainty and vagueness as compared to the existing Kruskal Wallis test under classical statistics. Finally, the results are discussed and generalized with some conclusive remarks.

Computational method of the modified Kruskal Wallis test under uncertainty

In Classical Statistics, nonparametric tests are methods of statistical analysis that do not require a distribution to meet the assumptions necessary to be analyzed. These tests apply to non-normal data sets. Due to this reason, they are sometimes referred to as distribution-free tests. The basic purpose of suggesting the Kruskal Wallis test is to scrutinize that all independent samples containing neutrosophic observations come from neutrosophic populations with equal means implying that the populations under uncertainty are identical. The proposed nonparametric test is applicable for data where the measure of uncertainty or the measure of falseness has been recorded. Suppose X N  =  a N  +  b N I N ; X N   ∈  [ X L ,  X U ] is a neutrosophic number where the first part represents the measure of determinacy and the second part represents the measure of vagueness or uncertainty. For  I N   ∈  [ I L , I U ] = 0, the neutrosophic number reduces to a random variable under classical statistics. The neutrosophic variable X N represents the neutrosophic sample obtained from the population containing imprecise, uncertain, and indeterminate observations; for detail, see ref [ 5 ].

Modified Kruskal Wallis H test

Under Classical Statistics, the Kruskal-Wallis H test is used to test the null hypothesis that all k independent samples come from populations having equal means against the alternative hypothesis that at least one population varies. The existing nonparametric test is a generalization of the two-sample Mann-Whitney U test. It is an extremely useful test when the assumptions of normality do not hold, or the population variances are not equal, but helpless for data under uncertainty. The modified Kruskal Wallis test under uncertainty will be applicable under the following assumptions:

The data consists of uncertain, imprecise, and indeterminate values.

The neutrosophic samples must be random.

The two neutrosophic samples must be mutually independent.

The test is generally considered robust to ties, but if there are ties in the data set, they shouldn’t be concentrated together in one part of the sample.

Suppose we have k N independent neutrosophic samples of sizes n 1 N , n 2 N , …, n kN  (∑ n iN  =  n N ). Let X iN  ( X i 1 N ,  X i 2 N ,  X i 3 N , …,  X inN ) represents the neutrosophic observations of the ith sample. To perform this test under uncertainty, arrange all the n N observations containing uncertainty of the k N samples combined in ascending order of magnitude and assign the ranks to them. In the case of ties, assign the average of the ranks. To distinguish the neutrosophic sample observations, let the letters A N , B N , C N , … represent the sample observations of the first, second, and third neutrosophic samples, respectively. The observations of the neutrosophic samples are replaced with their corresponding ranks. Add these ranks for each sample and denote the sums by R 1 N , R 2 N , …, R nk . Now compute

where r ijN is the rank assigned to neutrosophic observation X ijN ; X ijN   ∈  [ X ijL ,  X ijU ].If there are no ties, then

The modified Kruskal-Wallis statistic H N ; H N   ∈  [ H L ,  H U ] is given by

where C N ; C N   ∈  [ C L ,  C U ] denotes the appropriate correction term given by

In case of no ties, the neutrosophic statistic H N becomes

The neutrosophi form of the proposed test H N   ∈  [ H L ,  H U ] can be expressed as follows

Note here that the proposed statistic H N   ∈  [ H L ,  H U ] is a generalization of the existing test under classical statistics. The first part H L shows the determined part, H U I NH denoted the indeterminate part and I NH   ∈  [ I LH ,  I UH ] is the measure of indeterminancy/uncertainty. The proposed test reduces to the existing test when I LH =0.

The neutrosophic Kruskal Wallis H N test is used to test the null hypothesis that all k N populations have identical distributions. For a large value of the test statistic under uncertainty is rejected. For example, only three samples have five or fewer neutrosophic observations; the significance of this test statistic is determined by using Kruskal and Wallis’ Table [ 19 ] having critical values for all combinations of sample sizes up to 5,5,5. In case one of the neutrosophic samples contains more than five observations, or there are more than five observations in each neutrosophic sample and the null hypothesis is true, the neutrosophic test statistic H N follows a chi-square distribution with (k-1) degrees of freedom.

Application of the proposed modified Kruskal Wallis H test

For applying the proposed neutrosophic Kruskal Wallis test, data representing the daily ICU occupancy by Corona-positive patients have been considered, which was recorded specifically from Pakistan. The hypothesis under investigation for the research is to test a statistically significant the difference in the daily ICU occupancy of Covid-19 patients based on their age groups. Neutrosophy or uncertainty is introduced in the data for a better illustration. The neutrosophic Kruskal Wallis test is applied to test the null hypothesis that there is no difference in the daily ICU occupancy of Covid-19 patients among different age groups in Pakistan during December 2020. Daily ICU occupancy of Covid-19 patients aged 55 and above are shown in Fig. 1 , Daily ICU occupancy of Covid-19 patients aged 35–55 are shown in Fig. 2 and Daily ICU occupancy of Covid-19 patients aged 35 and below are shown in Fig. 3 .

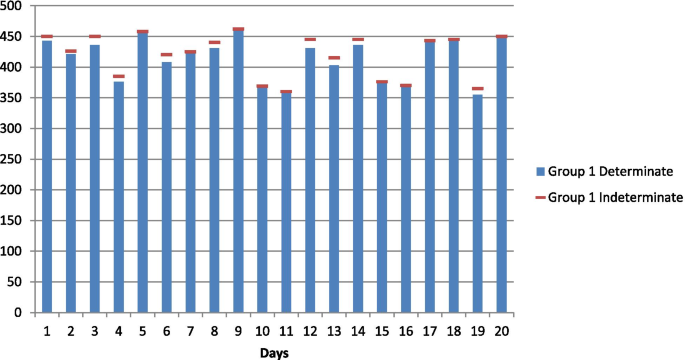
Daily ICU occupancy of Covid-19 patients aged 55 and above

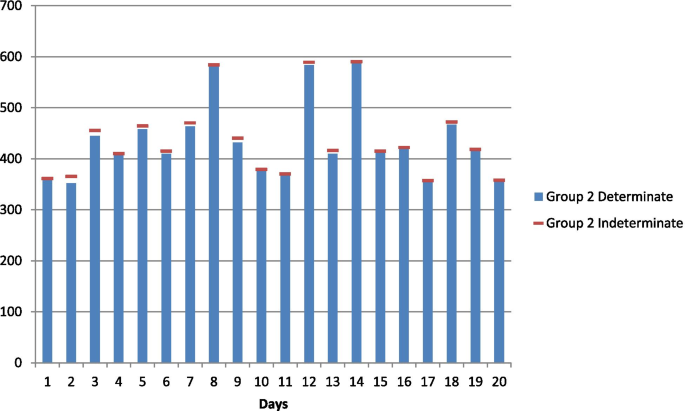
Daily ICU occupancy of Covid-19 patients aged 35–55

Daily ICU occupancy of Covid-19 patients aged 35 and below

The neutrosophic null and alternate hypotheses for neutrosophic data given in Table 1 are: The average daily ICU occupancy of Covid-19 patients for all three age groups are equal against the alternative hypothesis that the average daily ICU occupancy of Covid-19 patients for at least two of the three age groups are not equal. Table 1 contains data on daily ICU occupancy of Corona-positive patients by three different age groups. By combining and arranging the data in ascending order and assigning ranks to them, it is found that ties exist in the neutrosophic data set for both determinate and indeterminate parts. Therefore, the neutrosophic statistic is given in (4) applies to this data set containing the measure of uncertainty. Here R 1 N  = [757.5, 766.5], R 2 N  = [775.5, 767], R 3 N  = [297, 296.5], where R 1 N , R 2 N   and R 3 N represents the sum of ranks of age groups 1, 2, and 3, respectively.

From (1) and (2), we have

Assuming the level of significance to be 1%, the critical region is H N  >  χ 2 0.01,2  = 9.21. Since the calculated value of test statistic based on neutrosophic observations lies in the critical region ( p -value < α), we, therefore, reject the neutrosophic null hypothesis and conclude that daily ICU occupancy of different age groups of Covid-19 patients is not equal.

Advantages of the proposed test

In this section, the efficiency of the proposed test H N   ∈  [ H L ,  H U ] will be compared with the existing test under classical statistics in terms of a measure of uncertainty. As mentioned earlier, the neutrosophic H N  =  H L  +  H U I NH ; I NH   ∈  [ I LH ,  I UH ] has consisted of determinate (the existing test) and indeterminate parts. The neutrosophic form of H N   ∈  [ H L ,  H U ] for the real data is expressed as: H N  = 24.12 + 24.17 I NH ; I NH   ∈  [0,0.002]; where the first value 24.12 shows the results of the existing test when I LH =0 and 24.17 I NH is an indeterminate part. Note that the measure of indeterminacy associated with the test H N   ∈  [ H L ,  H U ] is 0.002. From the study, it can be seen that the proposed test the result of the test statistic in the range of 24.12 to 24.17. On the other hand, the existing test provides only the determined/exact value of the test. In addition, the proposed test H N   ∈  [ H L ,  H U ] gives information about the measure of uncertainty. Based on the information, the proposed test can be interpreted as follows: when the level of significance α =0.05, the chance of rejecting the null hypothesis when it is true is 0.05, the probability of accepting the null hypothesis is 0.95 with the chance of uncertainty of 0.002. From the comparisons, it can be concluded that the proposed test H N   ∈  [ H L ,  H U ] gives more information about the test. In addition, the proposed test is flexible, adequate, and effective to be applied in uncertainty as compared to the existing test.

Conclusion and discussion

This article proposed the modified form of the rank-based nonparametric Kruskal Wallis H test for observations containing the measure of uncertainty or the measurement of falseness when comparing k samples. It is evident from Table 1 that uncertain data used for the illustration purpose reduces to the determined part under classical statistics if no observations of uncertainty are logged. For example, for sample one, the first observation 443 for the first group represents the determinate part of the indeterminate interval. The second value, which is 450, represents the indeterminate part of the interval. We can observe here that the modified Kruskal-Wallis test results in the indeterminacy interval rather than the determined values, and this implies that the proposed test provides a good measure of uncertainty. Recent studies also show that the methods dealing with the interval-valued data are more suitable in the indeterminate environment than classical statistical techniques [ 25 , 26 ]. The work was originally motivated by the extensive research work under the fuzzy logic and neutrosophic statistics used for the interval-valued data set. The proposed nonparametric test can be readily applied to compare k samples testing the hypothesis that they have equal means.

The application of this new neutrosophic Kruskal-Wallis test on the Covid-19 data set showed that the proposed test provides more relevant and adequate results. The data representing the daily ICU occupancy by the Covid-19 patients were recorded for both determinate and indeterminate parts. The existing nonparametric Kruskal Wallis H test under Classical Statistics would have given misleading results. The proposed test showed that at a 1% level of significance, there is a statistically significant difference among the average daily ICU occupancy by corona-positive patients of different age groups.

The modified Kruskal Wallis test can be used to compare the averages of several sample observations or group(s); the proposed test is easy to apply and understandable. The Neutrosophic Kruskal Wallis test results in an uncertain interval, which is ideal when the data is measured from the complex system. The application of the proposed test is recommended for different fields, including biomedical sciences, engineering, and many other statistical areas. On the other hand, applying nonparametric tests under classical statistics on the data containing vagueness can produce misleading results. In conclusion, the proposed neutrosophic nonparametric test provides an efficient tool to data analysts for analyzing k samples in the presence of uncertainty and indeterminacy. However, more properties of this modified Kruskal-Wallis test can be derived for future research. The evaluation of the proposed test using different measures can be studied as future research.

Availability of data and materials

All data generated or analysed during this study are included in this published article.

Higgins JJ. An introduction to modern nonparametric statistics. CA: Brooks/Cole Pacific Grove; 2004.

Google Scholar  

Krzywinski M, Altman N. Nonparametric tests. Nat Methods. 2014;11:467–8. https://doi.org/10.1038/nmeth.2937 .

Article   CAS   PubMed   Google Scholar  

Chan Y. Biostatistics 102: quantitative data–parametric & nonparametric tests. Blood Press. 2003;140:79.

Buckley JJ. Fuzzy statistics: hypothesis testing. Soft Comput. 2005;9:512–8. https://doi.org/10.1007/s00500-004-0368-5 .

Article   Google Scholar  

Smarandache F. Neutrosophic Logic-A Generalization of the Intuitionistic Fuzzy Logic. Multispace & Multistructure Neutrosophic Transdisciplinarity (100 Collected Papers of Science). 2010;4:396.

Smarandache, F., Khalid, H. E. & Essa, A. K. Neutrosophic Logic: the Revolutionary Logic in Science and Philosophy. (Infinite Study, 2018).

Nabeeh NA, Abdel-Basset M, El-Ghareeb HA, Aboelfetouh A. Neutrosophic multi-criteria decision making approach for iot-based enterprises. IEEE Access. 2019;7:59559–74.

Abdel-Basset M, Nabeeh NA, El-Ghareeb HA, Aboelfetouh A. Utilising neutrosophic theory to solve transition difficulties of IoT-based enterprises. Enterprise Inform Syst. 2020;14:1304–24.

Abdel-Baset M, Chang V, Gamal A. Evaluation of the green supply chain management practices: a novel neutrosophic approach. Comput Ind. 2019;108:210–20.

Abdel-Basset M, Atef A, Smarandache F. A hybrid Neutrosophic multiple criteria group decision making approach for project selection. Cogn Syst Res. 2019;57:216–27.

Broumi, S., Bakali, A., Talea, M. & Smarandache, F. Bipolar neutrosophic minimum spanning tree. (Infinite Study, 2018).

Kruskal WH, Wallis WA. Use of ranks in one-criterion variance analysis. J Am Stat Assoc. 1952;47:583. https://doi.org/10.2307/2280779 .

McKight, P. E. & Najab, J. Kruskal-wallis test. The corsini encyclopedia of psychology, 1–1 (2010).

Hecke TV. Power study of anova versus Kruskal-Wallis test. J Stat Manage Syst. 2012;15:241–7.

MacFarland, T. W. & Yates, J. M. in Introduction to nonparametric statistics for the biological sciences using R 177–211 (Springer, 2016).

Soltani N, Safajou F, Amouzeshi Z, Zameni E. The relationship between body image and mental health of students in Birjand in 2016 academic year: a short report. J Rafsanjan Univ Med Sci. 2017;16:479–86.

Lou, Y., Yuen, S. Y. & Chen, G. in Proceedings of the Genetic and Evolutionary Computation Conference Companion. 1337–1341.

Muremi, L. & Bokoro, P. in 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe). 1–4 (IEEE).

Aslam M. A new goodness of fit test in the presence of uncertain parameters. Complex Intell Syst. 2021;7:359–65. https://doi.org/10.1007/s40747-020-00214-8 .

Aslam M. Introducing Kolmogorov–Smirnov tests under uncertainty: an application to radioactive data. ACS Omega. 2019;5(1):914–7.

Aslam M. Design of the Bartlett and Hartley tests for homogeneity of variances under indeterminacy environment. J Taibah Univ Sci. 2020;14(1):6–10.

Chen J, Ye J, Du S. Scale effect and anisotropy analyzed for neutrosophic numbers of rock joint roughness coefficient based on neutrosophic statistics. Symmetry. 2017;9:208.

Aslam M. Neutrosophic analysis of variance: application to university students. Complex Intelligent Syst. 2019;5(4):403–7.

Smarandache F. Introduction to neutrosophic statistics: infinite study. Columbus, OH, USA: Romania-Educational Publisher; 2014.

Meyer JP, Seaman MA. A comparison of the exact Kruskal-Wallis distribution to asymptotic approximations for all sample sizes up to 105. J Exp Educ. 2013;81:139–56.

Chen J, Ye J, Du S, Yong R. Expressions of rock joint roughness coefficient using neutrosophic interval statistical numbers. Symmetry. 2017;9:123.

Download references

Acknowledgments

We are deeply thankful to the editor and reviewers for their valuable suggestions to improve the quality of the paper.

Author information

Authors and affiliations.

College of Statistical and Actuarial Sciences, University of the Punjab Lahore, Lahore, Pakistan

Rehan Ahmad Khan Sherwani, Huma Shakeel, Wajiha Batool Awan & Maham Faheem

Department of Statistics, Faculty of Science, King Abdulaziz University, Jeddah, 21551, Saudi Arabia

Muhammad Aslam

You can also search for this author in PubMed   Google Scholar

Contributions

RAKS, HS, WBA, MF, MA wrote the paper. All authors read and approved the final manuscript.

Authors’ information

Corresponding authors.

Correspondence to Rehan Ahmad Khan Sherwani or Muhammad Aslam .

Ethics declarations

Ethics approval and consent to participate, consent for publication, competing interests, additional information, publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Sherwani, R.A.K., Shakeel, H., Awan, W.B. et al. Analysis of COVID-19 data using neutrosophic Kruskal Wallis H test. BMC Med Res Methodol 21 , 215 (2021). https://doi.org/10.1186/s12874-021-01410-x

Download citation

Received : 18 April 2021

Accepted : 23 September 2021

Published : 17 October 2021

DOI : https://doi.org/10.1186/s12874-021-01410-x

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Neutrosophic
• Fuzzy logic
• Kruskal Wallis H test

BMC Medical Research Methodology

ISSN: 1471-2288

• General enquiries: [email protected]

Kruskal-Wallis Test

• Reference work entry
• Cite this reference work entry

2351 Accesses

5 Citations

The Kruskal–Wallis test is a  nonparametric test that has as its goal to determine if all k populations are identical or if at least one of the populations tends to give observations that are different from those of other populations.

The test is used when we have k samples, with \( { k\geq 2 } \) , coming from k populations that can be different.

The Kruskal–Wallis test was developed in 1952 by Kruskal, W.H. and Wallis, W.A.

MATHEMATICAL ASPECTS

The data are represented in k samples. We designate by n i the dimension of the sample i , for \( { i = 1, \ldots,k } \) , and by N the total number of observations:

We class the N observations in increasing order without taking into account whether or not they belong to the same samples. We then give rank 1 to the smallest value , rank 2 to the next greatest value, and so on until N , which is given to the greatest value.

Let X ij be the j th observation of sample i , and set \( { i=1,\ldots,k } \) and \( {...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Kruskal, W.H., Wallis, W.A.: Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 47 , 583–621 and errata, ibid. 48 , 907–911 (1952)

Google Scholar  

Download references

Rights and permissions

Reprints and permissions

Copyright information

© 2008 Springer-Verlag

About this entry

Cite this entry.

(2008). Kruskal-Wallis Test. In: The Concise Encyclopedia of Statistics. Springer, New York, NY. https://doi.org/10.1007/978-0-387-32833-1_216

Download citation

DOI : https://doi.org/10.1007/978-0-387-32833-1_216

Publisher Name : Springer, New York, NY

Print ISBN : 978-0-387-31742-7

Online ISBN : 978-0-387-32833-1

eBook Packages : Mathematics and Statistics Reference Module Computer Science and Engineering

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• Registration Log In

Methodology and Application of the Kruskal-Wallis Test

This paper describes the methodology and application of the very popular nonparametric test which is a rank based test named as Kruskal-Wallis. This test is useful as a general nonparametric test for comparing more than two independent samples. It can be used to test whether such samples come from the same distribution. This test is powerful alternative to the one-way analysis of variance. Nonparametric ANOVA has no assumption of normality of random error but the independence of random error is required. If the Kruskal-Wallis statistic is significant, the nonparametric multiple comparison tests are useful methods for further analysis. The statistical analysis of the application data in this paper was performed with software MATLAB.

Periodical:

https://doi.org/10.4028/www.scientific.net/AMM.611.115

Cite this paper

Online since:

August 2014

Permissions:

Request Permissions

Сopyright:

© 2014 Trans Tech Publications Ltd. All Rights Reserved

* - Corresponding Author

[1] A.D. Aczel, Complete Business Statistics, Irwin, (1989).

Google Scholar

[2] D.C. Montgomery, G.C. Runger, Applied Statistics and Probability for Engineers, John Wiley & Sons, New York, (2003).

[3] E. Ostertagová, O. Ostertag, Methodology and Application of One-way ANOVA, in: American Journal of Mechanical Engineering, 2013, Vol. 1, No. 7, pp.256-261.

[4] W.H. Kruskal, W.A. Wallis, Use of Ranks in One-Criterion Variance Analysis, in: Journal of the American Statistical Association, 1952, Vol. 47, No. 260, pp.583-621.

DOI: 10.1080/01621459.1952.10483441

[5] J.D. Gibbons, S. Chakraborti, Nonparametric Statistical Inference, fourth ed., Taylor & Francis e-Library, (2005).

[6] E.B. Manoukian, Mathematical nonparametric statistics, Gordon and Breach Science Publishers, (1986).

[7] V. Bewick, L. Cheek, J. Ball, Statistics review 10: Further nonparametric methods, Critical Care, 2004, Vol. 8, No. 3, pp.196-199.

[8] W.J. Conover, Practical nonparametric statistic, third ed., John Wiley & Sons, New York, (1999).

[9] http: /www. statsdirect. com/help/default. htm#nonparametric_methods/kruskal_wallis. htm.

[10] D. Israel, Data Analysis in Business Research, first ed., Sage Publications Ltd, (2008).

Paper price:

After payment, you will receive an email with instructions and a link to download the purchased paper.

You may also check the possible access via personal account by logging in or/and check access through your institution.

This paper has been added to your cart

• For Libraries
• For Publication
• Policy & Ethics
• Privacy Policy
• All Conferences
• All Special Issues
• Read & Publish Agreements

© 2024 Trans Tech Publications Ltd. All rights are reserved, including those for text and data mining, AI training, and similar technologies. For open access content, terms of the Creative Commons licensing CC-BY are applied. Scientific.Net is a registered trademark of Trans Tech Publications Ltd.